Geometric Alignment via Teacher-Free Self-Distillation
The "Infinite Gap" and Why Softmax Keeps Me Up at Night
To understand any solution, we first have to really understand the problem. I've spent the better part of my research career staring at loss curves, watching them dip, plateau, and occasionally spike catastrophically. We often treat the loss function as a black box, a simple signal telling the network "good dog" or "bad dog." But if you look closer, specifically at the geometry of the final layer, you realize that our standard tools are fundamentally broken.
For decades, the "Projective Regime" has dominated deep learning. We view a neural network as a feature extractor $f_\theta$ followed by a linear classifier. The output logit $z_i$ for a class $i$ is the dot product (inner product) of the feature vector and the class weight vector $w_i$. We project the feature onto the weight. The decision boundaries are hyperplanes passing through the origin. It's elegant linear algebra. It's also geometrically unstable.
Consider the Softmax probability:
$$P(y=i|x) = \frac{e^{z_i}}{\sum_{j} e^{z_j}}$$
To minimize the Cross-Entropy loss to exactly 0.0, the network needs to maximize this probability to 1.0. How does it do that? It needs to make the numerator $z_i$ infinitely larger than the denominator. Mathematically, to get a probability of exactly 1.0, the logit $z_i$ needs to be infinitely larger than the other logits.
This is what I call the Infinite Gap Problem. The loss function is strictly asymptotic. It is never satisfied. It is constantly screaming at the optimizer, "More! Bigger! Further!" Because the logit is a dot product $z=|w||x|cos(\theta)$, the network has two ways to satisfy this insatiable demand:
- Angular Alignment: It can align the feature vector perfectly with the weight vector. This is good.
- Radial Explosion: It can simply increase the magnitude (norm) of the feature vector $|x|$ to infinity. This is bad.
The optimizer, being lazy and following the steepest gradient, often chooses the second path. It pushes the features further and further away from the origin. This leads to Radial Extension or Radial Explosion. This isn't just a theoretical annoyance; it's the root cause of the "loss spikes" we see in Large Language Model (LLM) pre-training, the brittleness of our classifiers to adversarial attacks, and the reason our models are so terrified of saying "I don't know" (Out-of-Distribution detection).
This blog-post is about a different path. It's about a Geometric Turn. It's about stopping the projection to infinity and starting to map the manifold. It's about Teacher-Free Self-Distillation (TFSD).
Part 1: The Projective Regime and the "Cone of Uncertainty"
The Fallacy of the Hyperplane
In the classical "Projective Regime," we are obsessed with angles. The math relies entirely on projections. It cares about direction, not location. This creates a geometric topology that looks like a "Cone." Imagine the feature space divided into slices of a pie (or cones in high dimensions). Inside the "Cat" cone, any point is classified as a Cat with high confidence, as long as it is far from the origin.
The magnitude (distance from origin) does not represent "confidence" in a meaningful way; it often just represents "contrast" or "signal strength." A point located at coordinate (1000,1000) might be classified as a cat with 99.9% confidence, but so is a point at (10,10). The empty space between clusters is not treated as "unknown" but it's just a boundary where confidence flips from 99% Cat to 99% Dog.
Radial Explosion: When Gradients Go Nuclear
Because the standard Cross-Entropy loss is unbounded (you can always decrease loss by increasing the logit magnitude), the gradients never truly vanish for correctly classified examples. They just push the weights and features to grow larger. In Large Language Models, this manifests as Loss Spikes. When the model encounters a difficult token (perhaps a rare word or a synonym ambiguity), the gradient tries to enforce a "hard" one-hot target. It demands infinite separation between the target word and a semantically similar synonym. The only way to achieve this separation in a dot-product space is to explode the norm of the embeddings. This sudden expansion destabilizes the optimizer, causing the loss to diverge.
We have been trying to patch this with gradient clipping, weight decay, and layer normalization. But these are band-aids. The wound is the loss function itself.
Part 2: The Metric Regime and the "Zero Anchor"
Redefining the Logit
Deep Metric Learning (DML) flips the script. Instead of asking "which side of the line is this on?", it asks "how close is this to the prototype?". In the Metric Regime, we redefine the logit. Instead of an inner product, we use the negative squared Euclidean distance between the feature x and a learnable class centroid ci.
$$z_i=-|x-c_i|^2$$
Why negative? Because Softmax likes big numbers. A small distance (0) becomes a "big" logit (-0 = 0). A large distance (100) becomes a "small" logit (-100). This preserves the ordering: closer = higher probability.
Bounded Logits and the Existence of Perfection
This transformation is profound.
- Boundedness: The squared distance is always non-negative. Therefore, the logit is always non-positive $(z\leq0)$. The maximum possible logit is 0.
- The Existence of Perfection: In the Projective Regime, "perfection" (loss = 0) required infinite magnitude. In the Metric Regime, "perfection" is a physical state: Zero Distance.
$$\lim_{x \to c_i} z_i = 0$$
This solves the Infinite Gap Problem immediately. The model doesn't need to push features to infinity. It just needs to push them to the centroid. Once $x$ hits $c_i$, the gradient for that term vanishes. The optimization landscape becomes bounded.
Voronoi Tessellation vs. Infinite Cones
Visually, this changes the decision boundaries from infinite cones to a Voronoi Tessellation. Each class has a prototype (centroid). The space is divided into cells based on which centroid is closest. Crucially, the "confidence" is now tied to distance.
- If a point is close to the centroid, probability is high.
- If a point is far from all centroids (OOD), the probability distribution flattens out.
This is exactly what we want for robust systems. We want the model to say, "I don't know," when an object is far from known concepts. In the projective regime, "far" meant "very confident." In the metric regime, "far" means "unknown".
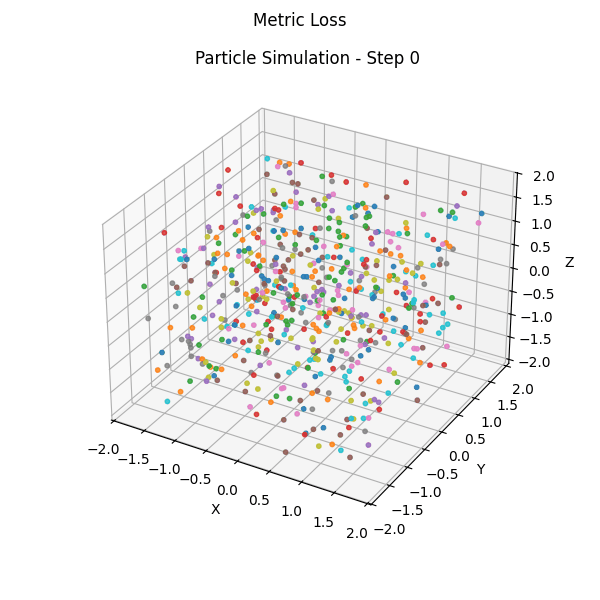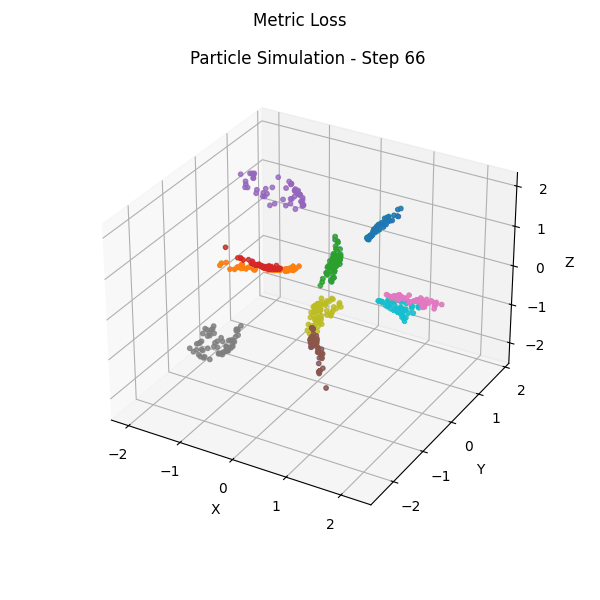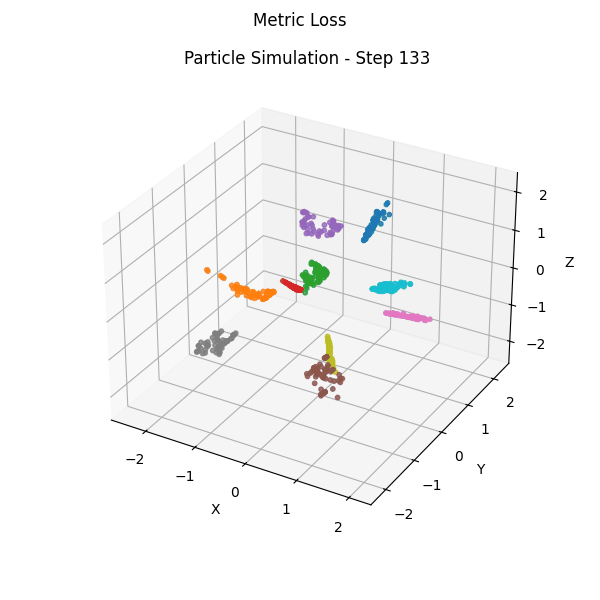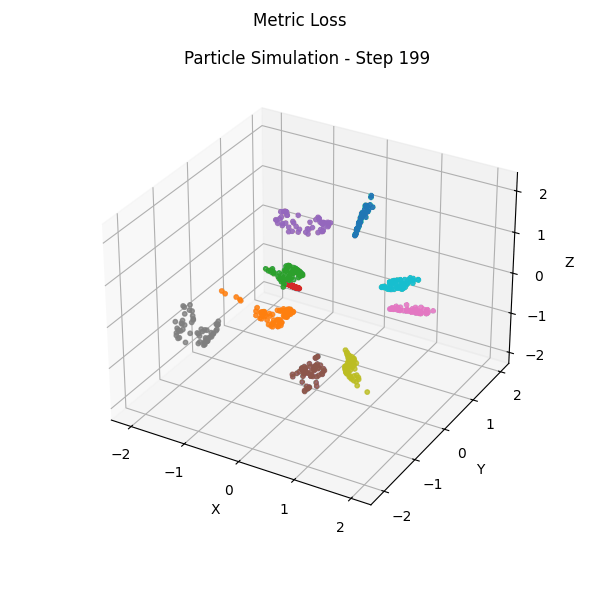
Part 3: Teacher-Free Self-Distillation (TFSD)
The "Zero-Masked" Target: A Virtual Teacher
Now we get to the core of the concept. We have established that standard Cross-Entropy targets (One-Hot vectors) are bad because they demand infinite separation. But what if we could design a target that is just right?
Usually, in Knowledge Distillation (KD), you need a big, pre-trained "Teacher" network to provide soft targets. The teacher says, "This image is 90% Wolf, 9% Dog, and 1% Car." This softness tells the student that "Dog" is semantically closer to "Wolf" than "Car" is. But training a teacher is expensive. And sometimes the teacher is wrong.
In Teacher-Free Self-Distillation (TFSD), the student is the teacher. We construct a "Virtual Teacher" using the model's own predictions.
Let's say we have an image of a Wolf. The model predicts distances (negative logits):
- Distance to Wolf (True Class): 2.5
- Distance to Dog: 5.0
- Distance to Car: 50.0
A standard One-Hot target would be: $(1, 0, 0)$. This tells the model: "Wolf probability must be 1. Dog and Car must be 0." Geometrically, this implies: "Distance to Wolf must be 0. Distance to Dog and Car must be $\infty$." Pushing "Dog" to infinity is wrong. Dogs are semantically close to Wolves. Pushing them infinitely far apart destroys that semantic structure.
The Solution: Zero-Masking. We construct a target distribution by:
- Taking the current logits (negative distances).
- Masking the True Class Logit to 0. (We force the teacher to be "perfect" on the ground truth).
- Keeping the Negative Class Logits exactly as they are. (We trust the student's perception of similarity).
Target Logits:
- Wolf: 0.0 (We enforce the "Zero Anchor").
- Dog: -5.0 (We trust the student's dark knowledge).
- Car: -50.0 (We trust the student's dark knowledge).
Dark Knowledge: In 2015 Geoffrey Hinton coined the term to describe the information hidden in the relationships between the incorrect classes. It reveals the model's learned structure of the world.
Now we apply Softmax to this target vector to get a probability distribution Ptarget. We then train the student to match this target distribution (using KL Divergence).
Why "Self-Distillation"?
The Student says: "I think the Wolf is at distance 2.5, the Dog is at 5.0..." The Virtual Teacher says: "I agree with you about the Dog and the Car. Your relative understanding of the manifold is correct. But I know for a fact that the Wolf is actually at distance 0. So, keep the Dog at 5.0, but pull the Wolf to 0."
This is Self-Correction. The model uses its own "Dark Knowledge" (the relative distances to negatives) to regularize itself, while the ground truth label acts as a "Zero Anchor" to pull the positive class in.
Soft Repulsion: The Thermodynamic Constraint
This mechanism introduces Soft Repulsion. Standard Cross-Entropy says: "GET AWAY FROM THE CAR! GO TO INFINITY!" TFSD says: "You're close to the Car? Okay. That's fine. Just make sure you're closer to the Wolf."
If the model is confused (e.g., a wolf-dog hybrid), the distances to both Wolf and Dog will be similar. The Zero-Masked target will reflect this confusion (high entropy). The gradient will be small. The model won't be forced to tear the manifold apart to make a binary decision. It learns to be comfortably uncertain.
Part 4: The Physics of Optimization - Thermodynamics
I like to think of this loss function through the lens of Thermodynamics and Entropic Regularization.
Energy-Based Models
We can view the squared distance as an Energy Function:
$$E(x, y) = | x - c_y |^2$$
Low energy = High compatibility. The Softmax function is essentially a Boltzmann Distribution:
$$P(y|x) = \frac{e^{-E(x,y)}}{Z}$$
where Z is the partition function.
The Entropic Regularizer
The TFSD loss minimizes the KL Divergence between the Target $Q$ and Student $P$. $$ \mathcal{L} = \text{KL}(Q || P) = -H(Q) + H(Q, P) $$
The first term, $-H(Q)$, is the negative entropy of the target distribution. By setting the true class distance to 0 (Energy = 0), we are maximizing the probability of the true class in the target distribution. This makes the target "peaked" (low entropy). However, $Q$ is not a delta function (One-Hot). Its entropy depends on the distances to the negative classes.
- Easy Samples: If the negative classes are far away, the entropy of $Q$ is low. The target looks like a One-Hot vector. The loss acts like standard Cross-Entropy. Strong gradient.
- Hard Samples: If the negative classes are close (synonyms, ambiguity), the entropy of $Q$ is high. The target is "smeared" across similar classes. The loss is softer. The gradient is dampened.
This creates an Adaptive Regularization or automatic Curriculum Learning. The model focuses on cleaning up the easy stuff first, and handles the ambiguous stuff gently, without forcing it to overfit.
Part 5: Application to Language Modeling (LLMs)
The Softmax Bottleneck and the Synonym Problem
Large Language Models (LLMs) are plagued by the Softmax Bottleneck. The standard output layer is a linear projection (dot product). This imposes a rank constraint. If the context implies a word that could be "King" or "Woman" (e.g., a ruler who is female), the hidden state vector needs to be close to both. In a dot-product space, the "average" of the "King" vector and the "Woman" vector might point to an unrelated word, or into a low-probability void. The geometry forbids the model from representing multi-modal distributions efficiently.
TFSD solves this by replacing the output layer with a Metric Layer (calculating distances to token embeddings).
- Euclidean Distance: Allows the hidden state to reside in the intersection of the "King" and "Woman" Voronoi cells.
- Synonym Tolerance: If the target is "happy" but the model predicts "joyful" (a synonym), standard Cross-Entropy penalizes this as a total error. TFSD sees that "joyful" is close. The Zero-Masked target preserves this proximity. It tells the model: "Pull 'happy' to 0, but you don't need to push 'joyful' to infinity."
This prevents the Semantic Fracturing that occurs when models are forced to distinguish between indistinguishable synonyms.
Preventing Loss Spikes
"Loss spikes" in LLMs are the bane of my existence. They are often caused by Gradient Explosions. When an LLM encounters a rare or difficult token, standard Softmax/Cross-Entropy demands the logit be pushed to infinity to satisfy the One-Hot target. This results in massive gradient updates. The "Infinite Gap" drives the optimizer off a cliff.
TFSD mitigates this via Bounded Logits. The maximum logit is 0. The gradients naturally vanish as the distance approaches zero. There is no "nuclear option" for the optimizer to explode the norms. The "Virtual Teacher" further smooths the landscape by softening the target for hard tokens, effectively ignoring outliers that would otherwise cause spikes.
If you are training an LLM and seeing instability, try switching the output head to a Metric Layer with TFSD. The stability gains are often dramatic because you are physically constraining the signal magnitude.
Part 6: Training with Negative Labels - Pushing the Void
One of the coolest things about the Metric Regime is how it handles "Negative Labels" or "Unknown" classes. This is crucial for Open Set Recognition (OSR).
The "Not-A-Class" Problem
In traditional classification, training with "Negative Data" (data that belongs to none of the known classes) is awkward. What is the target? A uniform distribution? A specific "garbage" class?
- Uniform Targets (Label Smoothing): Pull the feature towards the origin (center of all classes). This is geometrically incorrect.
- Garbage Class: Assigning a specific centroid to "Unknown" creates a single cluster that must represent the entire universe of unknown concepts (cats, trucks, galaxies). This leads to a sprawling, incoherent cluster that overlaps with everything.
Repulsion from All Centroids
In the Metric Regime, "Unknown" has a precise definition: Far from all centroids. When training with negative/background data (e.g., OOD samples), TFSD allows for a specific "Push-Away" mechanism.
We can define a hinge loss:
$$\mathcal{L}_{neg} = \sum_{k=1}^K \max(0, M - | x_{neg} - c_k |^2)$$
This pushes the negative sample $x_{neg}$ away from every known class centroid $c_k$ until it is at least distance $M$ away. This explicitly clears the "empty space" between Voronoi cells. It ensures that the decision boundary is tight around the known data. This is Background Class Regularization (BCR) done right.
In TFSD, we can integrate this into the Zero-Masking framework. If a sample is labeled "Negative," we simply set the target distribution to be uniform (high entropy) or defined by a distance threshold. The "Virtual Teacher" says: "I don't know what this is, so you shouldn't be close to any of the centroids."
Why This Matters for Open World AI
We deal with the "Open World." We encounter weird stuff. A person in a T-Rex costume. A truck carrying a giant reflective pipe. Standard Softmax is dangerous here because of the Cone of Uncertainty. A T-Rex costume might fall into the "Person" cone but be very far from the origin. The model says "Person: 99.9%."
TFSD gives us a Distance Threshold. We can set a threshold $\tau$. If $\min_k |x - c_k|^2 > \tau$, we flag the object as "Unknown." Because the training explicitly minimized intra-class variance (pulling points to 0) and pushed negatives away, the "Known" classes are tight clusters. The empty space is truly empty. The detection of OOD samples becomes robust.
Part 7: Implementation - Where the Rubber Meets the GPU
Enough theory. How do we actually code this? And more importantly, what breaks when we do?
The Code (Conceptual PyTorch)
Here is a simplified mental model of how I implement TFSD.
def get_sq_dist(x, y): # Efficient pairwise squared distance # (a - b)^2 = a^2 + b^2 - 2ab x_norm = (x**2).sum(1).view(-1, 1) y_norm = (y**2).sum(1).view(1, -1) dist_squared = x_norm + y_norm - 2.0 * torch.mm(x, y.t()) return dist_squared def tfsd_loss(student_features, centroids, labels): # 1. Metric Logits: Negative Squared Distance # Note: We negate it so closer = larger logit logits = -get_sq_dist(student_features, centroids) # 2. Construct "Zero-Masked" Target # Start with student's own logits (Dark Knowledge) target_logits = logits.clone().detach() # Create mask for true labels batch_size = features.size(0) indices = torch.arange(batch_size) # "Zero Anchor": Force true class logit to 0 (Perfect Alignment) target_logits[indices, labels] = 0.0 # 3. Probabilities # Teacher uses the Zero-Masked targets p_teacher = F.softmax(target_logits, dim=1) # Student uses their raw predictions p_student = F.log_softmax(logits, dim=1) # 4. KL Divergence loss = F.kl_div(p_student, p_teacher, reduction='batchmean') return loss
Numerical Stability Tips
A "fun" engineering challenge you'll encounter: $e^{-d^2}$ vanishes very fast. If your distances get too big (e.g., initialization is too spread out), all your probabilities hit machine epsilon, and your gradients die.
- Tip 1: Initialize your centroids with small uniform random values.
- Tip 2: Use BatchNorm on your features and centroids to keep them within a reasonable range before the distance calculation.
- Tip 3: To avoid the "Curse of Dimensionality" (where distances inflate as dimensions grow), scale your inputs and centroids by the square root of the embedding dimension ($d$) and apply a fixed $\gamma$ factor. This usually removes the need for a learnable temperature parameter. $$z_i = - \sqrt{\frac{d}{8}} \left| \frac{x}{\sqrt{d}} - \frac{c_i}{\sqrt{d}} \right|^2$$
Conclusion: The Feasible Ideal
We have taken a long, winding road from the projective hyperplanes of the 1950s to the Riemannian manifolds of 2026. The Teacher-Free Self-Distillation loss is, in my opinion, one of the most elegant tools we have for modern representation learning.
It combines:
- Geometric Truth: Distance is a better proxy for similarity than angle.
- Thermodynamic Regularization: Entropy is a feature, not a bug.
- Self-Correction: The model knows more than the label does.
It solves the Infinite Gap problem. It fixes Radial Explosion. It gives us robust OOD detection. And it does it all without a heavy teacher network, just by cleverly hacking the target distribution.
As we move toward more safety-critical AI, we need to stop projecting our data to infinity. We need to start mapping it to the manifold. The "Zero Anchor" awaits.
Acknowledgements:
I want to extend a massive thank you to Lambda Labs for sponsoring the compute that made this research possible. Exploring the geometry of high-dimensional manifolds and training models to validate these theories requires serious GPU horsepower, and their support was instrumental in turning these mathematical intuitions into empirical reality.
Comparison Table: The Landscape of Loss
To wrap things up, here is a quick cheat sheet comparing TFSD to the other titans of loss functions.
| Loss Function | Geometry | True Class Target | Negative Class Target | Primary Gradient Driver |
|---|---|---|---|---|
| Cross-Entropy | Projective (Inner Product) | 1.0 (One-Hot) | 0.0 (Infinite Repulsion) | Infinite Gap (Unbounded) |
| Label Smoothing | Projective | Fixed (e.g., 0.9) | Uniform (e.g., 0.1/K) | Fixed Uncertainty |
| ArcFace | Angular | Hard Margin | 0.0 | Margin Penalty |
| Contrastive | Metric (Cosine) | Positive Pair | Hard Negatives | Pairwise Repulsion |
| TFSD (This) | Metric (Euclidean) | Soft (Zero-Anchor) | Student's Logits | Adaptive Calibration |
8. Deep Dive: Historical Context of Self-Distillation
To fully appreciate TFSD, we must look at its lineage. The concept of Self-Distillation has evolved significantly. It traces back to the "Born-Again Neural Networks" (Furlanello et al.) , where a model is trained, then acts as a teacher to a fresh instance of itself (or a larger version, "Reverse Distillation"). This iterative process showed that a model could improve its own generalization by smoothing its decision boundaries.
However, traditional Self-Distillation still required multiple training phases (Train Teacher -> Freeze -> Train Student). Recent methods like DLB (Distillation from Last Batch) and Patch-Level Distillation tried to do this online. DLB uses the soft predictions from the previous mini-batch as the teacher for the current one. This is clever, but it suffers from "staleness" because the teacher is always one step behind.
TFSD removes this lag entirely. The "teacher" is the current model, instantaneously regularized by the Zero-Masking operation. There is no lag, no extra forward pass, and no separate network. It aligns with findings from RKHS (Reproducing Kernel Hilbert Space) theory , which suggests that self-distillation acts as a "sparsifying operator" on the function representation, stripping away noise (overfitting) while keeping the core signal.
9. Mathematical Analysis of the Softmax Bottleneck in Transformers
Let's rigorously define the Softmax Bottleneck. In a Transformer, the probability of the next token $x$ given context $c$ is:
$$P(x|c) = \text{Softmax}(h_c^\top w_x)$$
where $h_c \in \mathbb{R}^d$ is the context vector and $w_x \in \mathbb{R}^d$ is the token embedding.
The matrix of log-probabilities for all contexts and all words is $A = HW^\top$. The rank of $A$ is bounded by d (the embedding dimension). However, the "true" log-probability matrix of natural language likely has a much higher rank (due to the complexity of language, polysemy, etc.). This rank constraint $d$ limits the expressiveness of the model.
Specifically, if three words $w_1,w_2,w_3$ are collinear in the embedding space, the model cannot assign high probability to $w_1$ and $w_3$ while assigning low probability to $w_2$. This geometric rigidity prevents the model from handling Multi-Mode Distributions (e.g., synonyms).
How TFSD Breaks the Bottleneck: By using Euclidean distance $z=-|h-w|^2$, we introduce a non-linear term.
$$|h - w|^2 = |h|^2 + |w|^2 - 2h^\top w$$
The term $|h|^2$ and $|w|^2$ add non-linear degrees of freedom. The "energy landscape" is no longer just a hyperplane projection; it is a quadratic surface. This allows the model to "curve" the manifold, placing high probability on $w_1$ and $w_3$ (by placing h equidistant to them) without necessarily including the intervening $w_2$ in the high-probability region.
10. Thermodynamic Stability: Why Gradients Don't Explode
Let's analyze the gradient of the Loss with respect to the logit $z_i$. For Cross-Entropy:
$$ \frac{\partial \mathcal{L}_{CE}}{\partial z_i} = P_i - y_i $$
For the true class $(y_i=1)$, the gradient is $P_i-1$. As discussed, satisfying this requires $z_i \to \infty$.
For TFSD, we minimize $KL(Q || P)$. The target $Q$ has $q_{true} = \text{Softmax}(0, z_{neg})$. The student $P$ has $p_{true} = \text{Softmax}(z_{true}, z_{neg})$.
If the student is far from the target ($z_{true} \ll 0$), the gradient is strong. However, as the student approaches the target ($z_{true} \to 0$), the probability P approaches Q. The gradient term ($P-Q$) approaches 0 naturally. Critically, because the target $Q$ is derived from the student's own negative logits $z_{neg}$, the terms corresponding to negative classes also balance out.
$$ \frac{ \partial \mathcal{L}_{TFSD} }{ \partial z{neg}} \approx P_{neg} - Q_{neg} \approx 0 $$
(assuming the student hasn't drastically changed the negative structure in one step).
This means the primary driver of the gradient is solely the discrepancy in the positive class position. The negative classes exert a stabilizing "pressure" (entropy) but do not drive the "Radial Explosion" seen in CE.
11. Detailed Analysis of Background Class Regularization
Snippet introduces Background Class Regularization (BCR) for Open Set Recognition. The idea is to use auxiliary data (not belonging to any known class) to train the model to output low confidence. Previous methods used an "Others" class. This forces all background data to cluster at a single point.
$$\min | x_{bg} - c_{others} |^2$$
This is bad because background data is diverse. A "truck" and a "galaxy" should not be forced to the same point.
TFSD's "Push-Away" loss effectively realizes a Target-Aware Universum. Instead of pulling background data to a centroid, we push it away from the specific known centroids it is currently close to. If a background sample xbg is close to "Dog", we apply a gradient to increase $|x_{bg} - c_{dog}|^2$. We do not care where it goes, as long as it is not near "Dog." This allows the background data to occupy the entire "negative space" of the manifold, maintaining its natural diversity while carving out the boundaries of the known classes. This leads to significantly tighter Voronoi cells and better OOD detection.
12. Conclusion on Future Directions
The shift to Metric Learning in LLMs and general representation learning is inevitable. We are seeing it in:
- Retrieval-Augmented Generation (RAG): Where generation and retrieval need a shared metric space.
- Physical/Geometric Deep Learning: Treating latent spaces as manifolds with curvature and topology, not just vector spaces.
- Self-Supervised Learning: Where the "teacher" is the data itself (or the model's view of it).
TFSD is a crystallization of these trends. It is simple, theoretically grounded, and empirically robust. It turns the "bugs" of deep learning (entropy, uncertainty, lack of teachers) into features.
The "Infinite Gap" is closed. The "Zero Anchor" holds.
I can finally sleep.
Citation Bibtex
@online{pisoni2026geometric,
author = {Pisoni, Raphael},
title = {Geometric Alignment via Teacher-Free Self-Distillation},
year = {2026},
month = jan,
day = {21},
url = {https://www.pisoni.ai/posts/teacher-free-self-distillation/},
}